timohei.net / Opintojaksot / Opintojaksot / Aiemmin pitämäni opintojaksot / Näytejonosysteemit1 / Vanhoja tenttejä / Vanhoja tenttejä / 14.4.2005 /
Maksimipistemäärä
on 6+11+2 = 19 pistettä.
Vastaa
kaikkiin tehtäviin!
1
Mitä tarkoittavat seuraavat termit ja lyhenteet? Kirjoita
lyhyt kuvaus termin tai lyhenteen tarkoittamasta asiasta!
1.1
z-d![]()
![]()
z-d (2 p)
- viivetermi (1 p)
- d näytevälin pituisen viiveen z-muunnos (1 p)
- symboli järjestelmä- eli lohkokaaviossa
- z = e jw (˝ p)
1.2
siirtofunktion navat ja nollat (2 p)
- siirtofunktio H(z) on kahden polynomin osamäärä (˝ p)
- osoittajapolynomin (”yläkerran”) nollakohtia sanotaan siirtofunktion nolliksi
(˝ p)
- nimittäjäpolynomin (”alakerran”) nollakohtia sanotaan siirtofunktion navoiksi
(˝ p)
- navat ja nollat ovat kompleksisia
lukuja/taajuuksia (˝ p)
- siirtofunktio/amplitudivaste menee nollaksi siirtofunktion nollan taajuudella
ja äärettömäksi navan taajuudella (1 p)
- systeemin vahvistus kasvaa navan ja pienenee nollan lähellä (1 p)
- nollat merkitään nollanapakuviossa ympyrällä ja navat rastilla (˝ p)
1.3
amplitudivaste (2 p)
- systeemin vahvistus
taajuuden funktiona (1 p)
- taajuusvasteen itseisarvo (˝ p)
- aina reaalinen ja positiivinen (˝ p)
- voidaan arvioida systeemin nollien ja napojen sijainnin perusteella (˝ p)
2
Systeemin differenssiyhtälö on
![]()
2.1
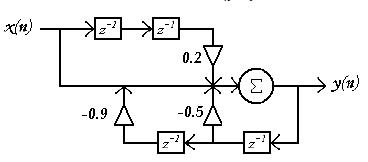
Piirrä systeemiä kuvaava järjestelmä- eli lohkokaavio! (2
p)
2.2
Määritä systeemin siirtofunktio H(z)! (2 p)

2.3
Määritä systeemin nollat ja navat sekä piirrä ne
yksikköympyrän kanssa kompleksitasoon! (2 p)


2.4
Laske systeemin vahvistus taajuuksilla ![]() = 0,
= 0, ![]() =
= ![]() ja siirtofunktion nollaa vastaavalla
taajuudella! (3 p)
ja siirtofunktion nollaa vastaavalla
taajuudella! (3 p)
Siirtofunktion nolla
sijaitsee imaginaariakselilla kulmassa +90o = p/2 radiaania, joten sitä vastaava kulmataajuus w = p/2.
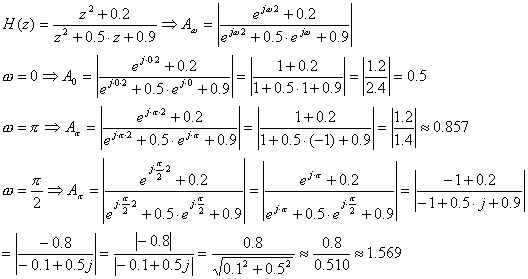
2.5
Piirrä systeemin amplitudivaste nolla-napa-kuviosta
päättelemällä! Käytä hyväksesi kohdassa 2.4 saamiasi tuloksia! (2 p)
Taajuusakseli ajatellaan
kiertyvän yksikköympyrän kehälle niin, että kohta, jossa yksikköympyrä leikkaa
positiivisen reaaliakselin, vastaa taajuutta 0 ja negatiivisen reaaliakselin
leikkaava kohta vastaa taajuutta p. Amplitudivaste voidaan arvioida kuljettamalla
tarkastelutaajuutta yksikköympyrän kehää pitkin taajuudesta 0 taajuuteen p, eli tasasignaalista näytteenottotaajuuden
puolikasta vastaavaan taajuuteen saakka.
Vahvistus on kohdan 2.4 laskelmien mukaan nollataajuudella 0.5, puolikkaan piin
kohdalla hieman reilu puolitoista ja piin kohdalla vajaa 0.9. Napa on hyvin
lähellä yksikköympyrän kehää, joten hieman piin puolikkaan jälkeen tulee
voimakas vahvistuspiikki. Taajuuksilla, joiden etäisyys nolliin ja napoihin on
suunnilleen yhtä suuri, vahvistus on noin yksi.

3
Diskreetistä signaalista on valittu analysoitavaksi
neljän näytteen pituinen jakso ![]() Laske jaksosta
DFT-muunnos, kun k=1. (2 p)
Laske jaksosta
DFT-muunnos, kun k=1. (2 p)
DFT-muunnos saadaan laskettua sijoittamalla sivun alalaidan kaavaan annetut
arvot. Näytejonon x(n) pituus N = 4, k = 1, ja itse näytejono x(n)
koostuu arvoista 0, -1, 0 ja 1.